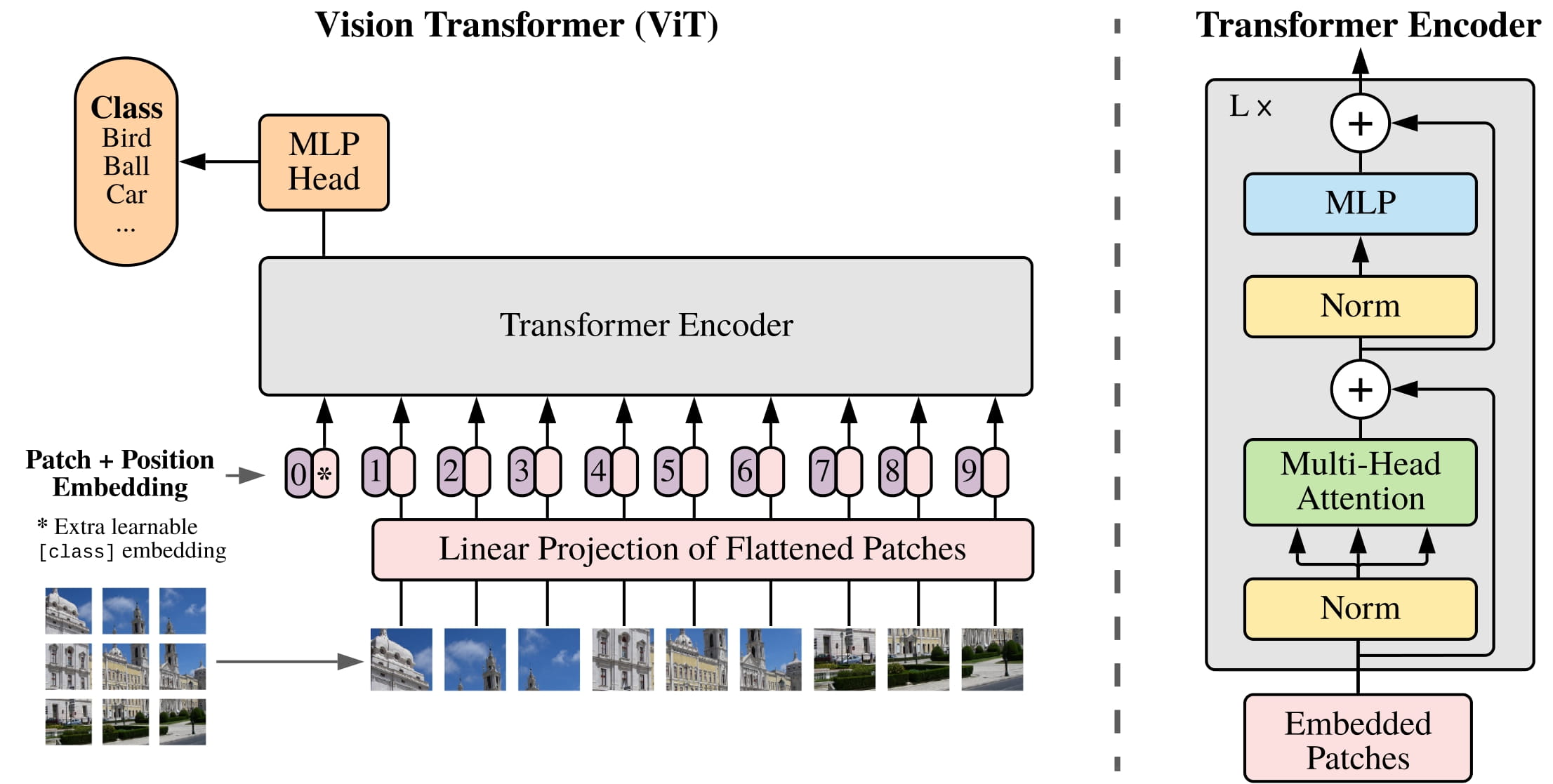
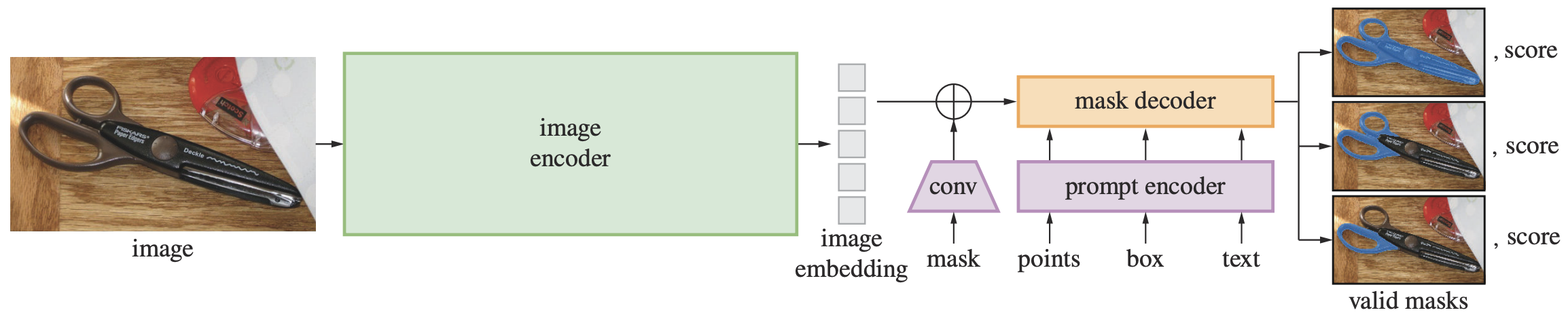
The Segment Anything Model (SAM) includes a powerful image encoder to compute the image embedding, a prompt encoder to create the prompt embedding, and a mask decoder that combines the two input embeddings to predict the segmentation mask. The image and prompt encoders are separate. Hence, the same image embedding can be reused with different prompts to amortize the cost. The mask decoder predicts multiple masks, so that it can handle ambiguity naturally.
As a side product, a new dataset SA-1B is released. It is 1B masks from 11M high resolution images that created by the model during training. The model was trained in multiple refinements, from human-assisted annotation to fully automatic.
Model Details
The model is described in Sec.3 of the paper with more details in Appendix A.
The image encoder is a masked autoencoder (MAE) pre-trained ViT adapted to process high resolution inputs.
The image encoder can be any network that outputs a $C\times H\times W$ embedding. The image encoder design in the paper follows Li et al (2022):
- ViT-H/16 with 14x14 windowed attention and 4 equally-spaced global attention blocks
- Input images are rescaled to 1024x1024 with padding the shorter side. Hence, the embedding is 64x64.
- 1x1 convolution to get 256 channels, then a 3x3 convolution to create the final embeddings. All convolutions are followed by layer norm
There are various prompt encoders depends on the type of prompts. The point, bounding box, and text are sparse prompts while masks are dense prompts. The points and boxes are converted into position encodings. Free-form text are converted into embeddings using the CLIP model. Dense prompts are processed with convolutions and summed element-wise with the image embedding.
Sparse prompts are mapped to 256-dim vectorial embeddings
- two learned embeddings to indicate if a point is foreground or background
- a point is the point’s positional embedding plus the foreground/background embedding
- a box is an embedding pair: top-left and bottom-right corners. There are two embeddings to indicate the two corners respectively. Each corner is the positional encoding plus such corner embedding.
- text uses the text encoder from CLIP
Dense prompts are input to the model at 4x lower resolution than the image, then downscale for another 4x using Conv2D(filter=4, kernel_size=2, stride=2), then Conv2D(filter=16, kernel_size=2, stride=2), then Conv2D(filter=256, kernel_size=1). Each Conv2D is separated by GELU and layer norm.
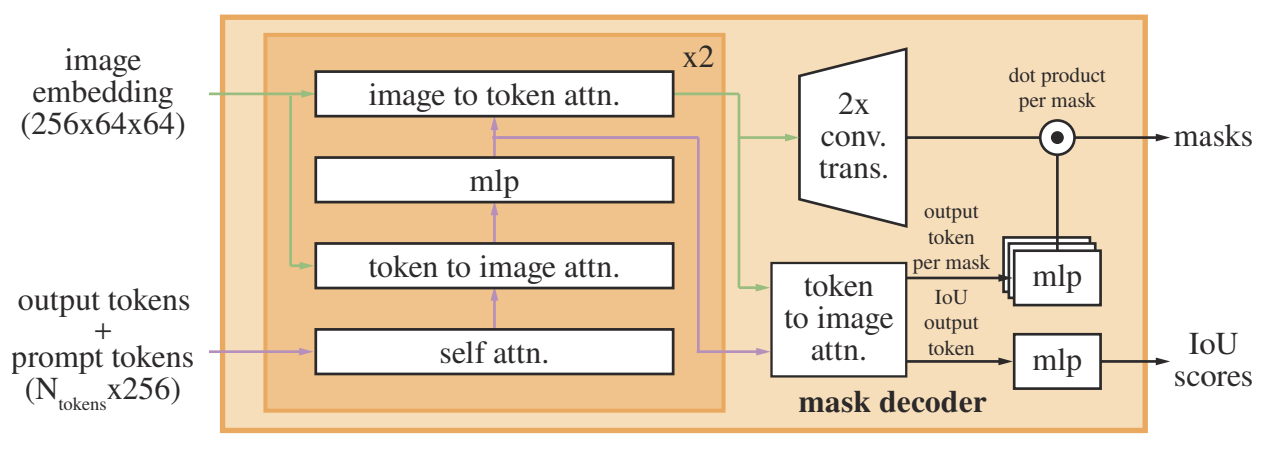
The mask decoder (figure below) is a transformer decoder block followed by a dynamic mask prediction head. The transformer decoder has prompt self-attention and cross-attention in two directions (prompt-image and image-prompt) to update all embeddings. MLP is used to map the output token to dynamic linear classifier, which then computes the mask foreground probability at each pixel.
The model outputs 3 masks, as a way to handle ambiguity. It is because nested masks are often at most three-deep: whole, part, and subpart. During training, backprop takes the minimum loss over all output masks, ranked using estimated IoU. The loss function is a linear combination of focal loss and dice loss.
The transformer decoder input sequence is the prompt embeddings and a learned output token embeddings analogous to the [cls] token in ViT. The image embedding is $64^2$ tokens each is a 256-dim vector. For multiple mask prediction, multiple (but distinct) learned output tokens are used.
The mask decoder has two decoder layers. Each decoder layer is in 4 steps: self-attention on the tokens, cross-attention from tokens to image, point-wise MLP on each token, and finally cross-attention from image to tokens. Each step is followed by residual connection, layer norm, and dropout (p=0.1). Attentions are 8 heads and using embedding dimension 256. MLP uses intermediate dimension 2048.
The output from image encoder is 16x downsampled from the input image. The output from mask encoder is then 4x upsampled by two transpose conv layers. Then, the output from mask encoder are attended once more to the image embedding, then processed by a 3-layer MLP to produce an output matching the conv-upsampled embedding. These two are combined in point-wise dot-product as final output.
Evolution: The Dataset
The model was trained in stages because the dataset to fit the model was not available.
At start, SAM was trained using common public segmentation datasets.
In the first stage, human annotators are to label pixel-precise masks using brush and eraser tools on a segmentation tool powered by SAM. The rule is to label “stuff” (mass nouns, such as snow) and “things” (count nouns, such as chair) as long as annotators can name or describe. The names are not collected. Then retrained SAM using only the newly annotated masks for 6 times, and scaled up from ViT-B to use ViT-H as image encoder.
The average number of masks per image increased from 20 to 44, collected 4.3M masks over 120K images.
The second stage aims to increase diversity of masks. Annotators are presented with images pre-filled with masks and asked them to annotate any additional unannotated objects. The model is then periodically retrained for 5 times on newly collected data.
The average number of masks per image increased from 44 to 72, and a total of 10.2M masks collected in 180K images.
The final stage is fully automatic. It is when enough masks are collected and the model can predict valid masks even in ambiguous cases. The model is prompted with a 32x32 regular grid of points and if the point lies on a part or subpart, the model will return the subpart, part and whole object.
IoU module selects confident and stable masks (i.e., same mask is produced when the threshold set to $0.5-\delta$ or $0.5+\delta$). Then apply non-maximal suppression to filter duplicates.
The result is a 11M images, downsampled to 1500 pixels on the shortest edge from photos of 3300x4950 pixels on average, with 1.1B high-quality segmentation masks. Compare to COCO, the images are 640x480 pixels only. The masks are model-generated. It is known that inter-annotator consistency is at 85-91% IoU (Gupta et al, 2019), but the machine generated masks has 90% IoU against the human annotator for 94% of the masks.
Training
Loss function is focal loss and dice loss added in 20:1 ratio. IoU prediction head is trained with MSE loss between IoU prediction and the predicted mask’s IoU with groundtruth.
Training is using AdamW ($\beta_1=0.9, \beta_2=0.999$), batch size of 256 images, no data augmentation, and linear learning rate warmup for 250 iterations, then step-wise learning rate decay. Initial learning rate after warmup is 8e-4. Training performed for 90K iterations or 2 epochs on SA-1B. Then decrease learning rate by a factor of 10 at 60K iterations and again at 86.6K iterations. For regularization, weight decay set to 0.1, drop path with rate of 0.4, and layerwise learning rate decay of 0.8.
Training was using 256 GPUs, splitting on using up to 64 randomly sampled masks per GPU. SA-1B masks that covered more than 90% of the image are discarded to improve results.
Implementation
The official repository is at https://github.com/facebookresearch/segment-anything and Hugging Face transformers library has another implementation. Note that the paper mentioned about text encoder using CLIP, the released code does not include that part.
The implementation in the transformers library is as follows.
The sample code from the documentation:
import torch
from PIL import Image
import requests
from transformers import SamModel, SamProcessor
device = "cuda" if torch.cuda.is_available() else "cpu"
model_id = "facebook/sam-vit-huge"
processor = SamProcessor.from_pretrained(model_id)
model = SamModel.from_pretrained(model_id).to(device)
raw_image = Image.open("path/to/image.png").convert("RGB")
input_points = [[[450, 600]]] # 2D location of a window in the image
inputs = processor(raw_image, input_points=input_points,
return_tensors="pt").to(device)
with torch.no_grad():
outputs = model(**inputs)
masks = processor.image_processor.post_process_masks(
outputs.pred_masks.cpu(), inputs["original_sizes"].cpu(),
inputs["reshaped_input_sizes"].cpu()
)
scores = outputs.iou_scores
and in processor(), you can pass on other prompts such as segmentation_maps (for mask input).
The model entry point is class SamModel in modeling_sam.py, and the processor SamProcessor is defined in processing_sam.py.
SamProcessor is not a model. It defined the __call__() function to encapsulate image and input prompts (points, labels, boxes) into a BatchFeature object. In the process, a SamImageProcessor object (defined in image_processing_sam.py) is used. Note that calling SamProcessor expects an image and optionally accept arguments input_points, input_boxes, and input_labels. But the input_labels is not for text labels. Rather, it is about the nature of the points (1=subject, 0=not subject, -1=background). If not specified, all points are assumed to use label=1. BatchFeature is a dict-like. Hence the model is called with model(**inputs). This is preprocessing only, namely, the image may be scaled but not encoded. You can find the full pixel values in the processor output.
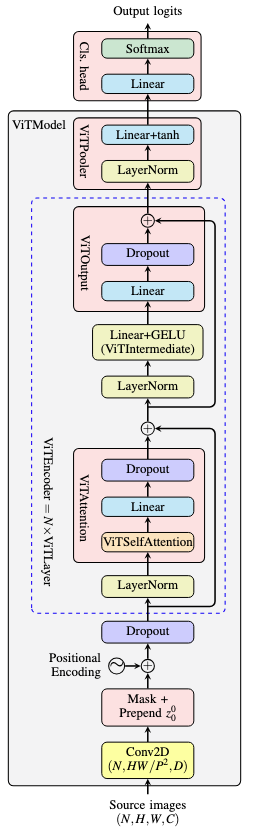
In SamModel, it instantiated SamPositionalEmbedding, SamVisionEncoder, SamPromptEncoder, and SamMaskDecoder. In forward() function,
- input pixels values are converted to embeddings using vision encoder (“last hidden state” is saved as the image embedding)
- input points, labels, boxes, or masks are converted into sparse and dense embeddings using the prompt encoder
- then the mask decoder takes the image embeddings, image positional embeddings, the sparse and dense embeddings to produce the low res mask, IoU predictions, and mask decoder attentions. These are wrapped as an object (
SamImageSegmentationOutput) for output.
SamPositionEmbedding set up the state using register_buffer(), which makes it not trainable. This is not the same as the position encoding for vision transformer used in the vision encoder.
In SamVisionEncoder, it instantiated SamPatchEmbeddings, a number of SamVisionLayer, and a SamVisionNeck
- input pixel is converted into embeddings by
SamPatchEmbeddingsclass, which usesnn.Conv2dwith kernel size and stride equal to patch size as in ViT model. The output is in the shape (N,H,W,C) - then positional embeddings is added to the image embeddings, which the positional embeddings is defined as
nn.Parameterof shape (1,H,W,C) in the constructor - then the image embeddings are processed by each vision layer
- finally the neck process the output from the last vision layer and the result is returned
SamVisionLayer is just a ViT layer, in which it is pre-norm, attention, residual connection, pre-norm, MLP, residual conneciton, and the result as output. Interestingly, the input image is maintained in spatial dimension, namely, in shape (N,H,W,C) instead of the usual (N,L,D) in transformer models. The norms are performed by nn.LayerNorm. MLP is implemented as SamMLPBlock, which is two linear layers with GELU activation in between. The attention is using SamVisionAttention class. In there:
# qkv with shape (3, batch_size, nHead, height * width, channel)
qkv = (
self.qkv(hidden_states)
.reshape(batch_size, height * width, 3, self.num_attention_heads, -1)
.permute(2, 0, 3, 1, 4)
)
# q, k, v with shape (batch_size * nHead, height * width, channel)
query, key, value = qkv.reshape(3, batch_size * self.num_attention_heads, height * width, -1).unbind(0)
The part self.qkv() projects the input tensor on the last dimension (C in NHWC). Then reshape convert the tensor to (N,L,3,h,d) format with h heads and d the dimension of each head. Then permuted to (3,N,h,L,d), reshape to (3,Nh,L,d) and unbind() to the Q, K, V tensors. Attention is then performed using these tensors. The result is then reshaped to (N,h,H,W,d), permuted and reshaped to (N,H,W,hd), then projected back to (N,H,W,C) shape to match the input.
SamVisionNeck is simply a Conv2D-layer norm-Conv2D-layer norm where nn.Conv2D is used but layer norm is implemented in SamLayerNorm, because nn.LayerNorm assumes “channel-last” but here needs “channel-first”.
SamPromptEncoder instantiated SamPositionalEmbedding, SamMaskEmbedding, and defined several nn.Embedding for no_mask_embed, point_embed, and not_a_point_embed respectively. It converts point, box, and mask into sparse and dense embeddings.
If points are provided, SamPositionalEmbedding is used to generate the point embedding. It is unclear in this version, but Meta’s implementation call it PositionEmbeddingRandom with the docstring “Positional encoding using random spatial frequencies.” Basically, it performs matmul on coordinate vector $(x,y)$ in shape $1\times 2$ (normalized coordinate to $[0,1]$) to random matrix of shape $2\times D$. Then the points are added with a “type” embedding based on labels, including background/subject/non-subject.
If boxes are provided, the two corners are extracted to generate the point embeddings. Then similar to the case of point prompts, type embeddings are added to denote the nature of the points.
If masks are not provided, a learned embedding is used as the substitute of the dense prompt. Otherwise, the mask is processed by the SamMaskEmbedding module. It is a model of two set of Conv2D-layer norm-activation then a final Conv2D to produce the embedding. Again, the layer norm is using SamLayerNorm to apply on the C dimension of NCHW tensors.
SamMaskDecoder instantiated two nn.Embedding (as IoU and mask tokens), two upscaling conv (nn.ConvTranspose2d), a SamLayerNorm layer, multiple SamFeedForward (as MLP blocks and the IoU prediction head), and a SamTwoWayTransformer.
It is invoked with image embeddings, image positional embeddings (representing the image size), sparse embeddings, and dense embeddings. At first, it created a concatenation of (IoU token, mask token, sparse prompt embeddings) as point embeddings. Then the dense prompt embeddings added to image embeddings. These two, together with the image positional embeddings are feed into the two-way transformer to extract new point and image embeddings.
The output image embeddings is upscaled (using conv-layer norm-activation-conv-activation). The first two token of the output point embeddings are extracted as output IoU and mask embeddings. The mask token is transformed with MLP. The upscaled image embedding and the MLP-transformed mask token are then multiplied (matmul) as mask output. The IoU token is transformed by the IoU prediction head (another feed forward block). These two are then returned as a tuple.
In pseudo-code:
def MaskDecoder(img_embed, img_pos_embed, sparse_embed, dense_embed):
point_embed = [iou_token, mask_token, sparse_embed]
img_embed = img_embed + dense_embed
point_embed, img_embed = TwoWayTransformer(point_embed, img_embed, img_pos_embed)
iou_out = point_embed[0]
mask_out = point_embed[1]
img_embed = img_embed.reshape() # NLD to NCHW
upscaled_embed = gelu(conv(gelu(layer_norm(conv(img_embed)))))
upscaled_embed = upscaled_embed.reshape() # NCHW to NDL
mask = (upscaled_embed @ mlp(mask_out)).reshape() # reshape NDC to NCHW
iou_pred = iou_pred_head(out_out)
return (mask, iou_pred)
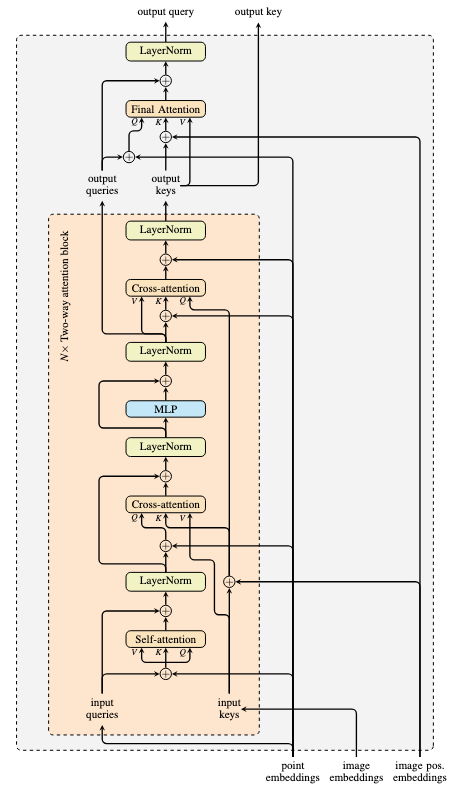
SamTwoWayTransformer is a stack of multiple SamTwoWayAttentionBlock and a final SamAttention block. The point embeddings and image embeddings were set as query and key respectively at start, and each layer takes query, key, and the original point and image positional embeddings to output new query and key. After the stack of two-way attention blocks, the final attention block processes query+point embedding and key+image positional embeddings. The output is then added back to query, processed by layer norm, and returned as the output point embeddings. The key embeddings (after image positional embeddings added) becames the output image embeddings. In pseudo-code:
def TwoWayTransformer(point_embed, img_embed, img_pos_embed):
img_embed = img_embed.flatten(2).permute(0,2,1) # NCHW to NLD
img_pos_emb = img_pos_embed.flatten(2).permute(0,2,1)
query, key = point_embed, img_embed
for attn_block in attn_block_layers:
query, key = attn_block(query, key, point_embed, img_pos_embed)
attn_out = final_attn(query=query+point_embed,
key=key+img_pos_embed,
value=key)
query = layer_norm(query + attn_out)
return (query, key)
SamFeedForward, which is used as the output mask token processor and the IoU prediction head, is a multi-layer of nn.Linear with ReLU activation.
In each SamTwoWayAttentionBlock, self-attention is first applied on query+point embedding, then post-norm on the query+output (addition for the residual connection) as new query. Then cross-attention applied on query+point embedding as Q and key+image position embedding as K and V. The output is added to query (as residual) and applied layer norm. Then output goes through SamMLPBlock, residual, layer norm. Subsequently, another cross attention using keys+image position embedding as Q, query (output from MLP+layer norm) as V, and that added with point embedding as K. It is a rare use of attention that all Q, K, V are distinct. The attention block output is added to keys and applied layer norm. The processed queries and keys are returned.
In graph, this is implemented as below:
References
- Masked Autoencoder: https://arxiv.org/abs/2111.063770
- Agrim Gupta, Piotr Dollar, Ross Girshick. LVIS: A dataset for large vocabulary instance segmentation. CVPR 2019.
- Yanghao Li, Hanzi Mao, Ross Girshick, Kaiming He. Exploring plain vision transformer backbones for object detection. ECCV 2022.