The LLaMA and LLaMA 2 model released by Meta/Facebook is available on GitHub and there’s a guide to help you using it. Of course, from Meta, this model is using PyTorch. But surprisingly, the repo on GitHub is very short that you can read and understand it in a day or two.
The structure of the repo is as follows. It is the LLaMA 2 model in its main branch. The older version is moved to another branch:
llama
├── __init__.py
├── generation.py
├── model.py
└── tokenizer.py
This is just the model code. To use it, such as to pretrain it from scratch (if you have such resources) or fine-tune it, you need to look into the scripts on the repo llama-recipes.
Tokenizer
All language model for text should start with a tokenizer that breaks a string
into tokens. In LLaMA 2, the tokenizer.py defines the class Tokenizer with
the encode() and decode() methods.
The LLaMA tokenizer uses SentencePiece model, which is based on BPE and Unigram. It added the BOS, EOS, and PAD as special tokens. The tokens are numbered as integer, which the encode and decode functions are to convert between a string and a list of such integers.
Parameters
There are several building block functions defined in the model.py
The static one is the dataclass ModelArgs, which holds the parameters for
inference or construction of the model. The default are:
dim= 4096n_heads=n_layers= 32max_seq_len= 2048, but this number is doubled in the model, hence effective sequence length limit is 4096
The building block functions are described one by one as follows:
Position encoding
The LLaMA model uses RoPE as the position encoding. Essentially it performs complex multiplication $xe^{it}$ for input $x$ and position $t$. The $e^{it}$ part is pre-computed and cached, up to the max sequence length, in the following function:
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
t = torch.arange(end, device=freqs.device)
freqs = torch.outer(t, freqs).float()
freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64
return freqs_cis
which the function torch.polar(x,t) computes $xe^{it}$, and $x=1$ here. The
output of this function is a tensor of shape $T\times D$. When it is used, the
input tensor is usually in the shape of $N\times T\times d$ for a batch of $N$
sequences. To perform element-wise multiplication of the position encoding
tensor and the input tensor, the following function is used to reshape the
position encoding tensor to fit the input tensor using view():
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
ndim = x.ndim
assert 0 <= 1 < ndim
assert freqs_cis.shape == (x.shape[1], x.shape[-1])
shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
return freqs_cis.view(*shape)
In most cases, the above function is to add a new dimension as the first axis to the position encoding. The actual rotary embedding operation is defined in another function:
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk)
The first two lines are to transform xq and xk from shape $(T,D)$ into
shape $(T,\frac{D}{2},2)$. Then the third line transforms the frequency tensor,
and finally xq_out is defined as the original xq_ elementwise multiply with
the position encoding, and take only the real part, and then reshaped back into
shape $(T,D)$.
The rotary embedding (RoPE) is explained as follows: The $d$-dimensional input vector $x$ is rearranged as $d/2$ pairs $(x_m^{(1)},x_m^{(2)})$. Here $m=1,\dots,T$ denotes the sequence position. Consider this as a coordinate pair in 2D plane, the transformation is to rotate with a constant angle $\theta$:
\[\textrm{RoPE}(x_m^{(1)},x_m^{(2)},m) = \begin{pmatrix}\cos m\theta & -\sin m\theta\\ \sin m\theta & \cos m\theta \end{pmatrix}\begin{pmatrix}x_m^{(1)}\\ x_m^{(2)}\end{pmatrix}\]The transformed output fulfills:
\[\begin{aligned} & \langle \text{RoPE}(x_m^{(1)},x_m^{(2)},m), \text{RoPE}(x_m^{(1)},x_m^{(2)},n)\rangle\\ = & \langle \text{RoPE}(x_m^{(1)},x_m^{(2)},m-n), \text{RoPE}(x_m^{(1)},x_m^{(2)},0)\rangle \end{aligned}\]which means the dot product is relative. In the implementation, we can consider $x$ at position $m$ is encoded as $xe^{im\epsilon}$ for some $\epsilon\in(0,\frac{\pi}{2N}]$. So the features $1,\dots,d$ will have feature $i$ pair up with feature $i+d/2$, and using angle $\theta_i = 10000^{-2(i-1)/d}$. The inner product above $\langle x, y\rangle = x\cdot \bar{y}$ is using complex inner product.
Lastly, to help multihead attention, there is a function to replicate the input
tensor x for n_rep times on the third dimension:
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
bs, slen, n_kv_heads, head_dim = x.shape
if n_rep == 1:
return x
return (
x[:, :, :, None, :]
.expand(bs, slen, n_kv_heads, n_rep, head_dim)
.reshape(bs, slen, n_kv_heads * n_rep, head_dim)
)
At input, the shape of x is (bs, slen, n_kv_heads, head_dim) and at output,
it becomes shape (bs, slen, n_rep*n_kv_heads, head_dim). The replication is
done as a view hence no new memory allocation.
Transformer building blocks
The overall transformer model is defined in the class Transformer, which has
the following workflow:
- The input
tokensis a tensor of token ids (shape of batch size $N\times$ sequence length $L$) andstart_posas integer- the parameter
start_posis for caching, useful in case of distributed model
- the parameter
- Convert
tokensinto embeddinghusingParallelEmbeddingmodule from fairscale (an PyTorch extension). The output tensorhis of dimension $d$ - Extract pre-computed encoding
freqs_cisat position rangestart_pos:start_pos+seq_lento match the input - Create a
maskof size $L\times L$ such that its upper triangular elements above offsetstart_posare all $-\infty$ and all other values are zero. This is the mask for causal inference. - There is a sequence of
TransformerBlock. Each block transformsh, with the other parameters:start_pos,freqs_cis, andmask. - Process the final
hwithRMSNorm - Apply
ColumnParallelLinearfrom fairscale with no activation function, which- the input
his a sequence of vectors of hidden dimension $d$ - the output is a sequence of logits of the length of the tokenizer vocabulary size
- the input
Fairscale is an alternative to
torch.nn.parallel.DistributedDataParallel (DDP) to do sharding on data,
model, and optimizer.
The building blocks to support the overall transformer architecture is as follows:
The class RMSNorm calculates
where the mean is applied on the square $x^2$ along the last dimension (i.e., embedding dimension). This is implementing the layer normalization.
The class Attention: This is where the parallelism applied in case of
distributed model execution
- defined weight matrices
self.wq,self.wk,self.wvto multiply withx- for the embedding dimension $d$ and number of query heads $H$, the attention dimension is $d_H = d/H$
- weight matrix $W^Q$ is of shape $d\times d$ but matrices $W^K,W^V$ are of shape $d\times H_{kv}d_H$, where $H_{kv}$ not necessarily equals to $H$
- defined weight matrix $W^O$ as
self.wofor output, as shape $d\times d$- same shape as $W^Q$, to make the output shape match the input shape
- defined
self.cache_kandself.cache_vas tensors of shape $(N,T,H_{kv},d_H)$ for batch size $N$, sequence length $T$, number of key/value head $H_{kv}$, and attention dimension $d_H$ - the workflow: takes input
x,start_pos,freqs_cis, andmask- input tensor of shape $(N,T,d)$ is transformed into $X_Q=W^QX, X_K=W^KX, X_V=W^VX$
- reshape $X_Q$ into shape $(N,T,H,d_H)$ and reshape $X_K,X_V$ into shape $(N,T,H_{kv},d_H)$
- apply rotary embedding on $X_Q,X_K$ with the tensor
freqs_cis - save $X_K,X_V$ on CUDA device and then replicate them for $n=H/H_{kv}$ times
- transform $X_Q$ and the replicated $X_K,X_V$ into shape $(N,H,T,d_H)$. At this point, all three tensors are in the same shape
- calculate the attention score $A=S(X_QX_K^\top / \sqrt{d_H} + M)$, where
- the inner product $X_QX_K^\top$ is multiplying along the $d_H$ dimension using
torch.matmul() - function $S(\cdot)$ is a softmax function, applied on the $T$ dimension of tensor $K$
- the mask $M$ is optional
- the argument to $S(\cdot)$ is of shape $(N,H,T,T)$, so as the output tensor $A$
- the inner product $X_QX_K^\top$ is multiplying along the $d_H$ dimension using
- then the output is calculated as $X_O = AX_V$
- tensor $A$ has shape $(N,H,T,T)$ and $X_V$ has shape $(N,H,T,d_H)$, the multiplication is along the last $T$ dimension of $A$ and the second last $T$ dimension of $X_V$
- multiplication done by
torch.matmul(A,Xv)and the output has shape $(N,H,T,d_H)$, which is then transposed into $(N,T,H,d_H)$. The resulting dimension $T$ is from a 1-to-1 matching between $X_Q$ and $X_V$
- Final output: $O = W^O X_O$, to bring back a tensor of dimension $d$
The class FeedForward: This is just a fully-connected layer used by TransformerBlock that computes
where:
- weight matrices $W_1,W_3$ are of shape $(d_{in},d_h)$ and matrix $W_2$ is of shape $(d_h,d_{in})$
- $d_h$ is specified in the
TransformerBlockas $4d_{in}$, but then adjusted to $\lfloor\frac23 d_h\rfloor$ and then round up to the multiple of a factor (e.g., 256)- for example: 13B model specified $d_{in}=5120$, then $d_h=13824$ ($\lfloor\frac83 d_{in}\rfloor = 13674$, then round up to multiples of 256); each saved model has 6912 with 2 shards
- $W_1,W_3$ are implemented as
ColumnParallelLinearand $W_2$ is implemented asRowParallelLinear; which onlyW_2has setgather_output=Trueto synchronize parallel runs
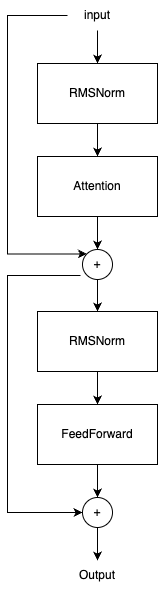
The class TransformerBlock: It connects a Attention module, a FeedForward
module, and two RMSNorm modules (one for attention and one for feedforward).
Its workflow is:
of which:
- pre-LN architecture is used, at both the attention and feedforward
- only self-attention but without cross-attention module as in the vanilla Transformer model, since this is a decoder-only architecture
- in diagram, it is as follows:
Generation Code
At generation.py, the class Llama and the function sample_top_p() are defined.
The function sample_top_p() takes a production distribution tensor probs and a probability threshold p as input. Then:
- Sorts
probsin descending order intoprobs_sort(and remembers the original index), then computes the cumulative sumprobs_sum - Find the mask
probs_sum - probs_sort > p; the mask at position $i$ means the cumulative probability of positions 0 to $i-1$ is strictly beyond $p$ - Zero out those masks in
probs_sort(i.e., position $i$ until the end) and renormalize it to make it sum to 1 - Random sample based on the renormalized probability distribution, then convert the sampled value to its original index
The class Llama ties everything together. In its constructor, it created a
Transformer object and a Tokenizer object. In the static factory method
build(), it takes inputs ckpt_dir (checkpoint dir), tokenizer_path,
max_seq_len, max_batch_size, model_parallel_size, and seed, and returns
a Llama object. In this build() function:
- it initialized
torch.distributedwith nccl backend (the only backend for GPU, the other backends gloo and mpi are for CPU only) - using
torch.manual_seed()to seed RNG to 1 - sort
*.pthfiles in the checkpoint dir; based on the current machine’s index in the distributed cluster, load the indexed file byget_model_parallel_rank()- the number of machines in a cluster must exactly match the number of shards in the checkpoint dir
- all checkpoints (e.g.,
consolidated.{00,01}.pth) are of the same byte size
- model parameters are loaded from
params.jsonfrom the checkpoint dir and updatesModelArgs, except the parametersmax_seq_lenandmax_batch_sizeare provided bybuild()only. Example:
{"dim": 8192, "multiple_of": 4096, "ffn_dim_multiplier": 1.3, "n_heads": 64, "n_kv_heads": 8, "n_layers": 80, "norm_eps": 1e-05, "vocab_size": -1}
- recreated
Tokenizerfrom thetokenizer_path, e.g., set the vocabulary size - create the
Transformerobject with the prepared arguments, then load the checkpoint. This works as one shard - create and return the
Llamaobject with theTokenizerandTransformermodels
In the Llama class, the method generate() is decorated with a PyTorch
inference mode decorator. It takes as input prompt_tokens (a batch of
prompts, as a list of list of vocab id), max_gen_len, temperature, top_p,
logprobs (boolean), echo (boolean). It returns the list of output tokens
(list of list of ids) as well as the corresponding logprob.
- at start, it validated that the input is within model’s max batch size and all prompts below the model’s max sequence length
- the model has been created. The pre-computed RoPE tensor cannot handle exceeding length
- the set
total_lento be the min ofmax_seq_lenandmax_gen_len + max_prompt_len; this should be the max output sequence length that this model can produce - the prepare tensors
tokens: tensor of size (batch_size,total_len) filled with the pad id, which is retrieved from the tokenizer- afterwards, fill in the
tokenstensor with the input prompts (left aligned)
- afterwards, fill in the
token_logprobs: tensor of size (batch_size,total_len) filled with zeroeos_reached: tensor of size (1,batch_size), filled with False to indicate if a prediction reached the EOS tokeninput_text_maskas boolean tensor to tell iftokensis not pad id
The workflow for generate() is as follows:
- if
min_prompt_lenreachedtotal_len, run the model once to get the logit, then calculatetoken_lgoprobsbased on the cross entropy between the logits and the original tokens - run autoregressively until
min_prompt_lenreachedtotal_len, with the position cursorcur_pos: a. if temperature=0, simply pick the next token by argmax b. if temperature > 0, use softmax andsample_top_p()to pick the next token c. next token is filled into the tensortokensat positioncur_posonly if it is masked d. then updatetoken_logprobsby comparing the model output logits to the “next token”- model is passed in the tokens of range
prev_pos:cur_posacross the batch to generate next token of each position; only the last output is used fornext_token, which correspond to the positioncur_pos+1 - initial
prev_posis 0; each iteration updatesprev_postocur_pos - comparing output logit to tokens of range
prev_pos+1:cur_pos+1tells how accurate is the model output using as much information as possible; all tokens atprev_pos+1:cur_pos+1are considered equally in cross entropy because the entire sequence is presented to the model e. updateeos_reachedto check if EOS has been generated atcur_pos; terminate the autoregressive for-loop if all input in the batch has EOS f. updateprev_postocur_posbefore next iteration - first iteration use subsequence from 0, subsequently, the input to the model is only the one token generated in the previous iteration
- this design is to minimize the computation:
- At second iteration onward, all tokens has been seen except the last
- Only the attention layer will need the entire sequence; the feedforward layer process each token individually.
- At attention layer, the start position is provided, which is used to update the key/value cache to insert the new token. Afterwards, the entire sequence can be read from the cache
- model is passed in the tokens of range
- at finish, convert the generated tensor
tokensinto list of tokens, cut off at EOS, optionally also produce the list of logprob - output: return the list of output tokens (list of list of ids) and logprobs
The methods text_completion() and chat_completion() are applications of
generate() method. Both takes the similar input as the last one (e.g.,
temperature, top-p) but in particular, in text_completion(),
- prompts are presented as a list of strings, then converted into a list of ids using the tokenizer in a loop
- then the converted prompts are passed to
self.generate()to get the generated tokens and logprobs - decode the generated tokens into string and return, optionally together with the logprobs
and in chat_completion(),
- prompts are presented as a list of
Dialogobjects, which in turn is a list ofMessage, a typed-dict ofroleandcontent - check if the Dialog contains any “unsafe” string, i.e., special tags (
[INST],[/INST],<<SYS>>,<</SYS>>) -
format the input: first message’s role can be “system”. If so, merge the first message with the second using the template
<<SYS>> {first message} <</SYS>> {second message} -
the list of dialog is assumed to have the prompt and answer interleaving; which then each pair is formatted as
[INST] {prompt} [/INST] {answer}and then the pairs are concatenated. The last message in dialog is the final prompt, also concatenated using the same template.
- the concatenated prompts are then tokenized and preserved in the list
prompt_tokensand sent toself.generate()
Execution
The repo has an example script, example_text_completion.py. This is not a
vanilla PyTorch code, but using fairscale. Hence you cannot run the script with
a barebone python interpreter. The suggested command (from its readme) is:
torchrun --nproc_per_node 1 example_text_completion.py \
--ckpt_dir ../llama-2-7b \
--tokenizer_path ../llama-2-tokenizer/tokenizer.model
The version in Hugging Face has these removed, hence we can run with the python interpreter directly. Example code:
from transformers import AutoTokenizer
import transformers
import torch
import accelerate
model = "meta-llama/Llama-2-7b-chat-hf"
tokenizer=AutoTokenizer.from_pretrained(model)
pipeline=transformers.pipeline(
"text-generation",
model=model,
tokenizer=tokenizer,
torch_dtype=torch.bfloat16,
trust_remote_code=True,
device_map="auto",
max_length=1000,
do_sample=True,
top_k=10,
num_return_sequences=1,
eos_token_id=tokenizer.eos_token_id
)
sequences = pipeline(
'Hi! I like cooking. Can you suggest some recipes?\n')
for seq in sequences:
print(f"Result: {seq['generated_text']}")
where trust_remote_code is required to download the weight from the hub, and
device_map should set to "auto" when using accelerate library. Other
parameters are to control the decoding strategies, such as multinomial
sampling, beam-search, top-K, and top-P. Only the beam-search and sampling
support num_return_sequences more than 1.
What is Fairscale?
It is an alternative to PyTorch DDP. It is a tool for sharding. To use:
- shard to optimizer: use wrapper
fairscale.optim.oss.OSS(optim=torch.optim.SGD, params=model.parameters, **otherargs)to create an optimizer instead of the simpletorch.optim.SGD; then replace the original model with wrapperShardedDDP(model, optimizer); afterward, runmodel.train()as usual - similarly, there are wrapper to parallelize models, e.g.
fairscale.nn.Pipe(model, balance=[a,b])to run a model across two GPUs such that the layers are loaded to each at a ratio of 2:1
In LLaMA-2 code, the parallelism is determined by the parameters WORLD_SIZE
and LOCAL_RANK, which the WORLD_SIZE should match the number of
checkpoints, e.g., 13B is 2. The model will have sharding on the number of
attention heads in the multi-head attention module.
- model is defined in the unsharded format, which the matrices are defined
using
ColumnParallelLinearandRowParallelLinear - in
Attentionclass,self.cache_kandself.cache_vare set up to the size of local heads to manage thexkandxv(i.e., key and value tensors) - As
ColumnParallelLinearis used forwq,wk, andwv, the optiongather_output=Falsemakes all matrix multiplication local; asRowParallelLinearis used forwo, the output is gathered, and specifiedinput_is_parallel=True - example: 13B model, 2 shards, model param
dim=5120,n_heads=40,n_layers=40. Based on the code, the attention dimensionhead_dimshould be 5120/40=128 and the matrices $W^Q,W^K,W^V,W^O$ should be all 5120×5120 (after input vector multiplied with matrices, reshape it to (40,128) for attention score computation). But in the.pthfile, these matrices are of shape 5120×2560.