Koch snowflake is probably the simplest fractal graphic. The fractal idea is to draw a straight line segment, \(x_0-x_1\), and make the trisection points \(x_{1/3}\) and \(x_{2/3}\). Then replace the segment \(x_{1/3}-x_{2/3}\) with a equilateral triangle, like the image below.

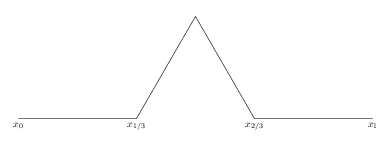
This way, what was one line segment becomes four shorter segments. Each segment can undergo the same change. Each iteration will make the number of line segments increase to four times the original. Hence it is exponential to the number of iterations done.

Coordinate geometry

Consider a program to make this. Assume we have a line segment from coordinates \((x_0,y_0)\) to \((x_1,y_1)\), the trisections are at \((x_a,y_a)\) and \((x_b,y_b)\) which

The apex of the equilateral trangle \((x_c,y_c)\) can be thought of point \((x_b,y_b)\) rotated for an angle of \(\theta=\pi/3\) about \((x_a,y_a)\). We can then first translate the coordinate system to \((x_a,y_a)\) as origin and apply the rotation matrix to \((x_b,y_b)\), and restore the origin, i.e.,

It is obvious that \((x_0,y_0)\) and \((x_1,y_1)\) swapped will make the triangle up side down. Hence we must be careful about the order of the coordinates in presentation.

tkinter code

I can’t find a simpler way than write this in Python with tkinter (whole thing in <100 lines!). Now consider what we need:

• A GUI to draw a line, as the basis for the whole fractal
• The GUI should better provide a resizable canvas
• Click on the canvas will evolve the fractal for one iteration

We can worry about more complicated UI issues later.

Let’s denote a coordinate by a tuple of two floats. The above rotation-by-\(\theta=\pi/3\) formula can be written as:

def rotpi3(xa,ya,xb,yb):
    sin, cos = math.sqrt(3)/2, 0.5
    xc = cos*(xb-xa) - sin(yb-ya) + xa
    yc = sin*(xb-xa) + cos(yb-ya) + ya
    return xc, yc

and trisection:

def trisec(x0,y0,x1,y1):
    xa,ya = (2*x0+x1)/3.0, (2*y0+y1)/3.0
    xb,yb = (x0+2*x1)/3.0, (y0+2*y1)/3.0
    return xa,ya,xb,yb

Now comes the UI construction. Tk is simple. You need a root window (abstract UI canvas), a frame (window object with title bar and borders), and a canvas enclosing each on in such order. Then you can run the app until it quits:

import Tkinter as tk

class koch(tk.Frame):
    def __init__(self, root):
        tk.Frame.__init__(self, root)
        self.lines = []
        self.objs = []
        self.pack(fill=tk.BOTH, expand=True)
        self.canvas = tk.Canvas(self)
        self.canvas.pack(fill=tk.BOTH, expand=True)
        self.canvas.bind("<Configure>", self.on_resize) # resize event
        self.canvas.bind("<ButtonPress-1>", self.on_down) # mouse down
        self.canvas.bind("<B1-Motion>", self.on_drag) # mouse drag

root = tk.Tk()
root.title("Koch snowflake")
root.geometry("640x480") # init size
_ = koch(root)
root.mainloop()

We hook up the canvas to three events. The configure event is for window resizing. We want to resize the canvas when the window resized. The other two are for mouse button press down and drag. This is the behaviour for drawing a line on the canvas. We will also overload the mouse down event to evolve the fractal. Below is the full implementation:

import Tkinter as tk
import math

class koch(tk.Frame):
    def __init__(self, root):
        tk.Frame.__init__(self, root)
        self.lines = []
        self.objs = []
        self.pack(fill=tk.BOTH, expand=True)
        self.canvas = tk.Canvas(self)
        self.canvas.pack(fill=tk.BOTH, expand=True)
        self.canvas.bind("<Configure>", self.on_resize) # resize event
        self.canvas.bind("<ButtonPress-1>", self.on_down) # mouse down
        self.canvas.bind("<B1-Motion>", self.on_drag) # mouse drag
    def on_resize(self, event):
        "Change canvas size and clear the canvas"
        self.canvas.config(width=event.width, height=event.height)
        self.clear_canvas()
    def on_down(self, event):
        "Mouse down: remember the position and evolve if we already drew a line"
        self.x0, self.y0 = float(event.x), float(event.y)
        if self.objs:
            self.evolve()
    def on_drag(self, event):
        "Mouse drag: clear the canvas and draw a new line"
        x1, y1 = float(event.x), float(event.y)
        self.lines = [(self.x0, self.y0, x1, y1)]
        self.draw()
    def clear_canvas(self):
        for lineobj in self.objs:
            self.canvas.delete(lineobj)
        self.objs = []
    def draw(self):
        "Clear canvas, draw every line segments and save the object"
        self.clear_canvas()
        for coords in self.lines:
            self.objs.append(self.canvas.create_line(*coords))
    def evolve(self):
        newlines = []
        for x0,y0,x1,y1 in self.lines:
            xa,ya,xb,yb = trisec(x0,y0,x1,y1)
            xc,yc = rotpi3(xa,ya,xb,yb)
            newlines.extend([(x0,y0,xa,ya),(xa,ya,xc,yc),(xc,yc,xb,yb),(xb,yb,x1,y1)])
        self.lines = newlines
        self.draw()

def rotpi3(xa,ya,xb,yb):
    sin, cos = math.sqrt(3)/2, 0.5
    xc = cos*(xb-xa) - sin*(yb-ya) + xa
    yc = sin*(xb-xa) + cos*(yb-ya) + ya
    return xc, yc

def trisec(x0,y0,x1,y1):
    xa,ya = (2*x0+x1)/3.0, (2*y0+y1)/3.0
    xb,yb = (x0+2*x1)/3.0, (y0+2*y1)/3.0
    return xa,ya,xb,yb

root = tk.Tk()
root.title("Koch snowflake")
root.geometry("640x480") # init size
_ = koch(root)
root.mainloop()

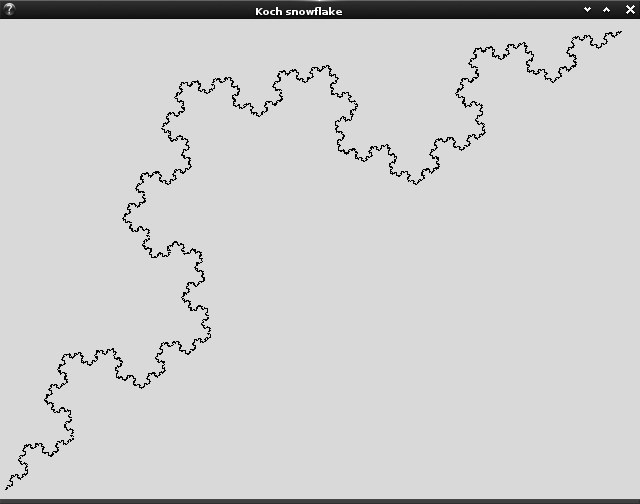
Screenshot:

Further work

First thing we notice is that the canvas is in an inverted coordinate such that the coordinate \((0,0)\) is at top left corner. We can separate the drawing coordinate system from the canvas coordinate system. Doing so will allow more intersting feature such as zooming or moving. But this also means we have to remember the transformation between the two, i.e., we need these functions:

class koch():
    def cartesian2canvas(self, x, y):
        can_x = (x - self.xLL) / (self.xUR - self.xLL) * self.width
        can_y = (self.yUR - y) / (self.yUR - self.yLL) * self.height
        return can_x, can_y
    def canvas2cartesian(self, x, y):
        cart_x = float(x)/self.width * (self.xUR - self.xLL) + self.xLL
        cart_y = self.yUR - float(y)/self.height * (self.yUR - self.yLL)
        return cart_x, cart_y

The snowflake doesn’t quite like a snowflake because we start with a straight line. It would be much prettier if we start with three straight line instead, namely, step zero in the form of a equlateral triangle. This is easy to do

def on_drag(self, event):
    "Mouse drag: clear the canvas and draw a new line"
    x1, y1 = float(event.x), float(event.y)
    x2, y2 = rotpi3(self.x0, self.y0, x1, y1)
    self.lines = [(self.x0, self.y0, x2, y2), (x2, y2, x1, y1), (x1, y1, self.x0, self.y0)]
    self.draw()

We can also limit the fractal to such that if each line segment is less than a pixel size, we do not further evolve it. This prevents (in certain sense) the app from being unresponsive.

Furthermore, we can not only hook up to mouse events but also keyboard events. However, doing so for canvas is tricky: you need to put the focus to canvas after it is created or otherwise it will not see it, as focus is supposed for input widgets like text boxes:

class koch():
    def __init__(self.root):
        self.canvas.focus_set()

Doing all these does not make the code enormously larger. It is now located at https://github.com/righthandabacus/pykoch