Hypercycloid, hypocycloid, and more general version, the hypertrochoid and hypotrochoid, are curves of the locus of a point on a circle rolling on a bigger circle. Like many other locus problems, it is convenient to tackle it from parametric equations.
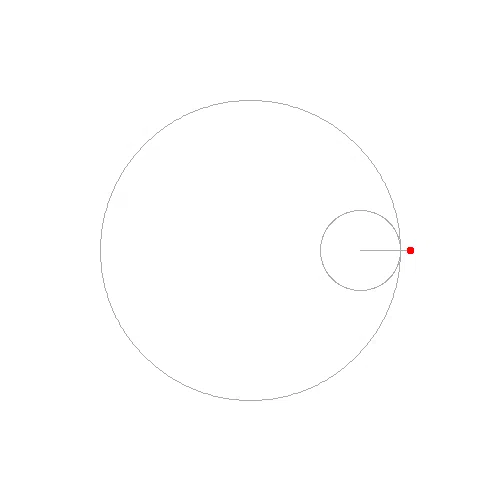
We go with the hypercycloid (aka epicycloid) first. Consider the image below from Wikipedia, we have a bigger circle of radius \(R\) with centre fixed at the origin. The smaller, rolling circle of radius \(r\) is rolling on the outside of the circle such that there is always a single point of intersection between the two circles. The locus of interest is drawn by point \(P\) on the smaller circle while it rolls.
Observe that when the smaller circle is rolling, its centre always follows a circle of radius \(R+r\) centred at the origin. Assume at the moment that the smaller circle rolled to the position such that its centre is at angle \(\theta\) as illustrated, the length of arc it has rolled is \(R\theta\). This is the same length measured on the big or small circle. Assume point \(P\) is the point of contact of the two circle when \(\theta=0\). At the moment of an unspecified \(\theta\), the point \(P\) is at the angle of \(\alpha = R\theta/r\) relative to the point of contact of the two circle at the moment, or at the angle of \(\alpha+\theta\) relative to the \(x\) axis (such angle is measured at the third quadrant).
Given that we have the coordinate of the centre of the smaller circle to be
\[\begin{align} x &= (R+r)\cos\theta \\ y &= (R+r)\sin\theta \end{align}\]and the coordinate of the point \(P\) to be
\[\begin{align} x &= (R+r)\cos\theta - r\cos(\frac{R+r}{r}\theta) \\ y &= (R+r)\sin\theta - r\sin(\frac{R+r}{r}\theta) \end{align}\]and more generally, if point \(P\) is on a circle of radius \(\rho\) eccentric to the smaller circle, then the parametric formula of the locus of the hypertrochoid (aka epitrochoid) is:
\[\begin{align} x &= (R+r)\cos\theta - \rho\cos(\frac{R+r}{r}\theta) \\ y &= (R+r)\sin\theta - \rho\sin(\frac{R+r}{r}\theta) \end{align}\]The derivation is similar if the smaller circle is rolled on the inside of the bigger circle. Except that the angle of point \(P\) relative to the \(x\) axis when the centre of the smaller circle is at angle \(\theta\) is \(\alpha-\theta\) (measured at the first quadrant), as now the point is on the clockwise side rather than counterclockwise side when the smaller circle rolled. So similarly, the parametric equation of hypocycloid is:
\[\begin{align} x &= (R-r)\cos\theta + r\cos(\frac{R-r}{r}\theta) \\ y &= (R-r)\sin\theta - r\sin(\frac{R-r}{r}\theta) \end{align}\]and the more general version, hypotrochoid, is:
\[\begin{align} x &= (R-r)\cos\theta + \rho\cos(\frac{R-r}{r}\theta + \phi) \\ y &= (R-r)\sin\theta - \rho\sin(\frac{R-r}{r}\theta + \phi) \end{align}\]In above, we added an angle \(\phi\) to \(\alpha\) such that we allow a version rotated about the origin. The shape, however, should be just the same.
Now some code. I like the animated GIF on wikipedia page that shows how the locus is created as the parameter \(\theta\) goes from 0 up to some big angle. Generating such animation is indeed not hard, as we already derived the coordinates and metrics of everything need to show. I will use Python, for its Pillow library is handy to create such pictures. And in addition to GIF, I can also generate animated image in Google’s WebP format. Here is the code (python 3.6+ required due to type hint syntax):
and this is the command to generate a hypercycloid:
python3 hypchoid.py -q 180 hyper.webp
and this is for a hypochoid:
python3 hypchoid.py -p 50 -o hypo.webp